

Searching for Search
Searching for Search
Searching for Search
Conjecture
Nov 28, 2022
Thanks to Dan Braun, Ze Shen Chin, Paul Colognese, Michael Ivanitskiy, Sudhanshu Kasewa, and Lucas Teixeira for feedback on drafts.
This work was carried out while at Conjecture.
This post is a loosely structured collection of thoughts and confusions about search and mesaoptimization and how to look for them in transformers. We've been thinking about this for a while and still feel confused. Hopefully this post makes others more confused so they can help.
Mesaoptimization
We can define mesaoptimization as internal optimization, where “optimization” describes the structure of computation within a system, not just its behavior. This kind of optimization seems particularly powerful, and many alignment researchers seem to think it’s one of the biggest concerns in alignment. Despite how important this is, we still understand very little about it.
For starters, it's not clear what internal optimization actually means. People have proposed several definitions of optimization which fit well when thinking about “behavioral optimization” where an agent acts to optimize its environment. One of the most clear and popular definitions comes from Alex Flint:
an optimizing system is a physical process in which the configuration of some part of the universe moves predictably towards a small set of target configurations from any point in a broad basin of optimization, despite perturbations during the optimization process.
In this framing, an agent and its environment together form an optimization process, where the agent acts upon the environment such that the system as a whole robustly converges to a set of target states.
But we run into problems when we try to map this behavioral definition to a definition about the structure of a process's internal computation. When we say mesaoptimization, we seem to mean something different than just that the computation converges to a smaller target. For example, an image classifier takes a large set of initial configurations of images including a lot of noise and irrelevant details, and layer by layer narrows it down to a probability distribution concentrated on a single class prediction. There seems to be a sense that this is not doing the kind of optimization we are concerned about when we talk about mesaoptimization.
Mesaoptimization was originally defined in Risks from Learned Optimization as internal search:
We will say that a system is an optimizer if it is internally searching through a search space (consisting of possible outputs, policies, plans, strategies, or similar) looking for those elements that score high according to some objective function that is explicitly represented within the system.
An advantage of this framing is that we do have some idea what we mean by “search” and have concrete examples of things which unambiguously qualify. Ideally, we’d like to point to the more general class of computation we’re worried about, but once you start thinking about what this general class of computation might look like, it quickly becomes clear that we don’t even know what “search” is. The space of search algorithms also seems much larger and more flexible than implied in the examples we usually think of.
At the moment we have very little idea what kind of algorithms we should expect neural networks to learn, and neither do we have a good picture of what kind of algorithms in particular we should be concerned about when we think of misalignment. If the intuition that “search” is somehow central to internal optimization holds validity, then becoming less confused about what learned search looks like should be central to making risks from internal optimization more concrete.
What is Search?
We have examples of processes which most would say are doing some kind of search, like Monte Carlo tree search, or A*, and processes that not everyone agrees count as search, like evolution through natural selection or stochastic gradient descent, which nonetheless clearly have search-like properties (the general disagreement about these examples is evidence that the concept is confusing). Some of these prototypical examples are handcrafted, others are natural, but broadly they operate in a similar way: They tend to generate candidate solutions, have a method for evaluating these candidate solutions, and use those evaluations to do a kind of iterative refinement of the solution space. This is highly reminiscent of what Abram Demski calls selection processes, which are able to both instantiate members of the solution space and obtain direct feedback on their quality.
While these are clearly doing search, this doesn’t look at all like how humans usually do search. Humans don’t restrict themselves to enumerating and evaluating candidate solutions. Instead, humans often operate over highly abstract compressions of the solution space, or search over entirely different spaces, such as global constraints on the problem, to make finding a solution more tractable.
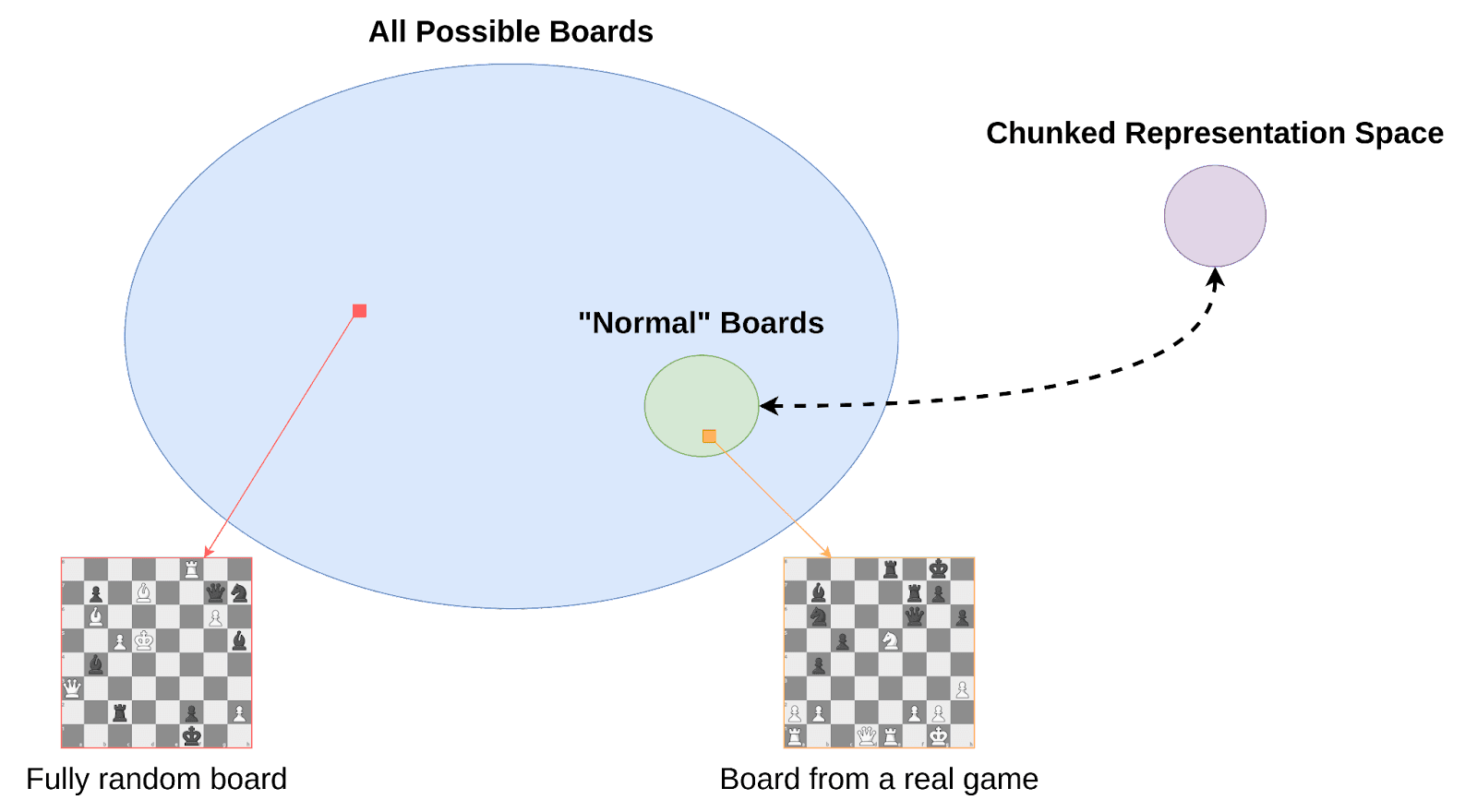
Instead of focusing on one particular type of search, we want to think about the general properties that our examples of search share. At the highest level, they each take a large space of possible candidates (generally implicit to a problem specification) and shrink it down to a single solution which satisfies some criteria. If we say a process which finds a solution from a space of 2^N candidates can be thought of as doing N bits of optimization, then one place to start is to ask where those bits of optimization come from.
Compressing the search space
By transforming the search space into one which has significantly fewer degrees of freedom, we can quickly obtain a large number of bits, and shrink the scope of the problem down to one which is much more manageable.
Master chess players are able to better memorize boards by chunking structures of pieces as single units and converting a board to a higher level concept space not possessed by novices.[1] For instance, instead of separately tracking the positions of every pawn, the master player might memorize a single position for a group of pawns in a commonly-occurring arrangement.
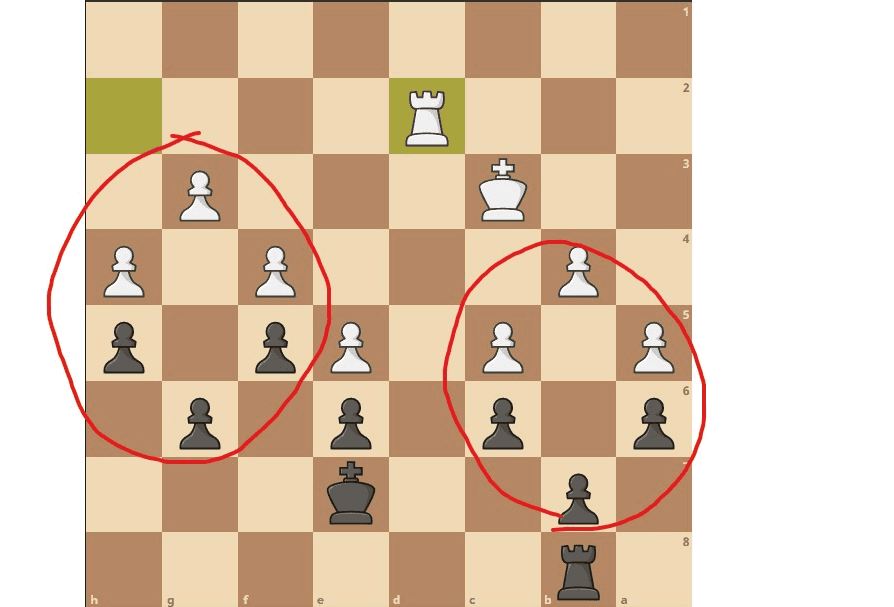
This advantage is only present for real game positions, however, and completely disappears for fully random board states. This suggests that the concept space used by master players implicitly ignores most of the possible ways that the pieces can be arranged, and therefore has less degrees of freedom than the original space did. (It has to: for any lossless compression scheme, some possible sequences are inevitably incompressible, because there are fewer sequences of length < N than length N.)
Furthermore, unlike concepts representing literal "chunks" of relative positions parameterized by absolute position, many useful concepts may be invariant to the exact position of the pieces, like the concept of a “pin” or “skewer”. In practice this is a type of lossy compression which would not be able to disambiguate between possible boards if the differences are unlikely to be strategically relevant. The compression, more generally, is just a useful ontology, which makes the search problem significantly easier. Promising candidates (board positions or sequences of positions) can be represented in fewer bits, and the lower dimensional representation space can be used as a generator of candidates, because satisfactory solutions now make up a larger fraction of the now smaller compressed space.
This is important, because the way that the solution space gets compressed will shape what search looks like from the inside. Evaluated candidates may not be in the naive or expected representation, but rather be pointers to pieces of an internal ontology that might look very different. We should also expect those internal representations to be harder to detect and decipher, because the more a representation gets compressed, the more we should expect it to lose structural correlations which might distinguish it from noise.
Searching over constraint space
Another way to reduce the number of degrees of freedom is to focus on the constraints of a search problem. Searching over global constraints has many advantages, and seems to be one of the main ways humans search when the solution space is too large to reason about directly. Constraint space tends to be much lower dimensional, and can be used to implicitly carve out huge chunks of the original solution space, or break a problem down into smaller subproblems, allowing a search process to recurse on those subproblems, factoring the problem into manageable pieces. In a game like chess this might look like searching for threats, which operate like bottlenecks, requiring all successful plans to involve mitigating the threat as an instrumental subgoal.
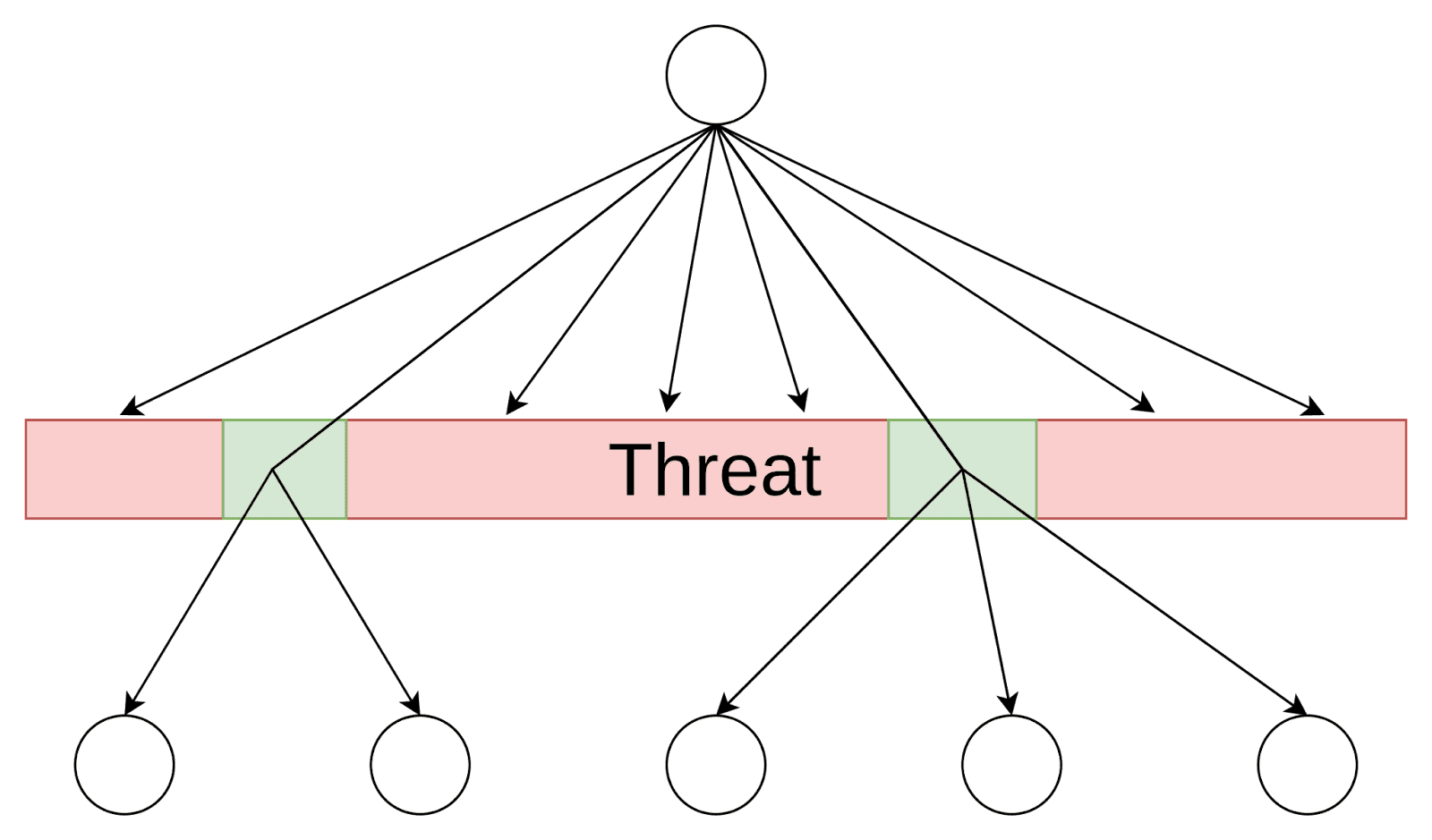
This means that the candidates being considered may not map to solutions at all, instead being objects of an entirely different search space (e.g. that of threats). A search process might also consider solutions to smaller or relaxed subproblems, and never reference or relate directly to the full search target. This affects the problem of searching for search, because we might not be able to find the algorithm if we only search for signs of a search over solution space, such as instantiations of candidate solutions.
Another important quality of constraint space is that constraints are often useful for a wide range of search targets. For example, when planning a long distance trip, any successful plan will likely require booking a flight and going to the airport. This fact doesn’t depend very much on the exact destination, and so is especially useful to a more general purpose search process.
General purpose search, of the kind that humans possess, is also the kind of internal optimization that is most concerning and worth our study. Such a system would need to be able to take a search problem and actively simplify it by finding exploitable features of the search space at runtime, and breaking that problem down into more manageable subproblems.
Modularity and Retargetability
General purpose search needs to be able to take on a wide range of possible search problems and be flexible to distributional shifts. Systems which are robust to changes in the objective tend to be modular, composing their computation into submodules.
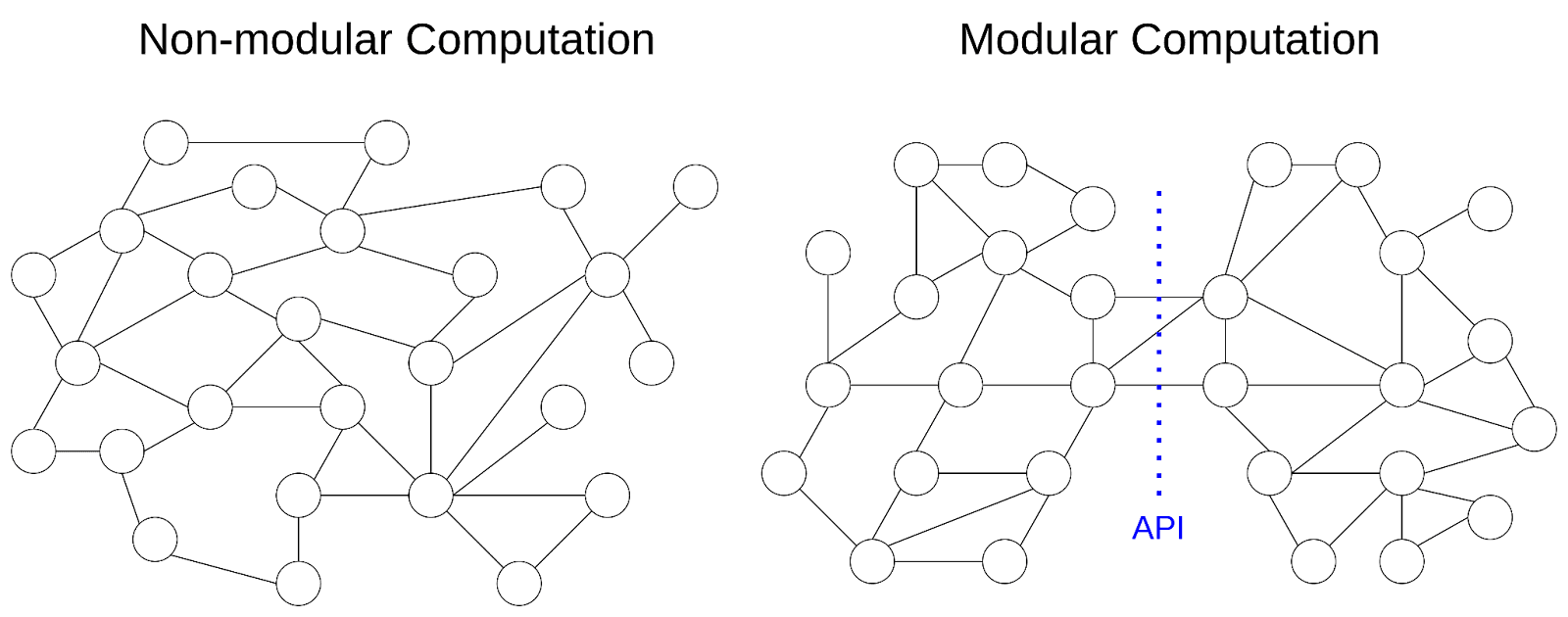
Non-modular systems, where the dependencies of computation are spread too widely to be split into distinct modules, are more likely to be brittle to changes in how the computation is performed. In learning to code, for example, a common early lesson is to split a program up into functions, and allow each function to interact with the rest of the program only through a small number of input and output variables (and avoid references to global variables). This doesn’t just make code easier to read, which is not a requirement for learned algorithms, but more importantly it contains the ripple effect that a change in one function has on the rest of the program.
This advantage of modularity applies both at runtime (reducing the chances that an uncommon input causes failure), as well as during development (reducing the number of changes needed to fix a bug). Analogously, we might expect modularity in learned algorithms both for their ability to generalize at runtime, as well as a part of the inductive bias of gradient descent. The more sprawling the dependencies, the more directions in the gradient landscape will lead directly to machinery breaking (and thus higher loss). A change to a module, on the other hand, need only be accompanied with a change to the API for the system as a whole to keep on functioning.
A likely place to find an example of modularity is in the retargetability of a search algorithm. If a search algorithm is general purpose, then the “target”, or what is being searched for, can’t be baked into or be implicit to the search process, but rather must be an input to a retargetable search algorithm. This applies to a system capable of handling a broad set of search problems, but even systems trained only to search with a single target have an incentive to be retargetable if that search algorithm breaks the problem down into subproblems, each with their own instrumental targets. If internal to the system there exists a target-agnostic search algorithm, with separate machinery for providing the target, then one place to start would be to find those modules (and understand how they interact with each other).
What even is a target/goal?
A target, through its interaction with the search algorithm, functions to “steer” search toward converging to a particular set of solutions. Much of the search process might be possible to do without any reference to the target (goal-agnostic preprocessing), but for general purpose algorithms we should expect a significant amount of the computation to hinge pivotally on the target.
In handcrafted search algorithms, the target has a clear type signature, and its interaction with the rest of the search process is well understood. In MCTS, for example, the target takes the shape of an evaluation function, and similarly for A*, the target is a coordinate which is used by a heuristic distance metric to guide the search process. They are both retargetable algorithms, and it’s easy to see how changing the target will change the process by which the algorithm will narrow the search space.
In learned search, it might be searching over multiple different ontologies, many of which don’t map to the solution space, as well as generate instrumental goals and recurse on subproblems. We don’t currently know what type signature the target would have, or how it slots into a search process to guide the computation, because we don’t have a good gears-level understanding of what learned search looks like.
Developing a better understanding of what targets are, both conceptually and experimentally, might give us a foot in the door toward understanding how targets interact with other modules within the search algorithm.
Learned Search in Transformers
Another angle of attack to understand mesaoptimization and search is to think about what types of algorithms we expect neural networks to learn. “Learned search” refers to search algorithms which, unlike handcrafted search algorithms, have been found automatically via gradient descent. If we find learned search within neural networks, it will need to conform both to the limitations of what can be implemented in the architecture as well as the inductive bias of gradient descent. Because of the success of LLMs like GPT-3 I’ll be focusing on the transformer architecture. Many of the arguments also apply to other architectures.
We might expect mesaoptimizers to be preferred for many reasons. Search at runtime is effectively a compressed version of a more complicated policy that encodes the information gained by search explicitly, specifying a system capable of generating that policy. For example, instead of memorizing a book of optimal chess openings, a program much shorter than the book could search through future consequences of moves and hypothetically converge to the same output.
There are, however, some reasons to be skeptical of finding search in transformers.
First of all, search isn’t free: the chess program that does brute-force search may have fewer lines of code, but is more expensive to run than a program that simply looks up a memorized answer. Any search algorithm which uses too much computation or memory just cannot be implemented by a transformer. This rules out many of the algorithms which rely heavily on explicitly enumerating and evaluating states. In the same vein, any algorithm that requires a high number of serial steps would also not be possible to run, even if the algorithm itself is in principle quite simple to describe. Unlike the NLP architectures that came before it, transformers are not recurrent. Information can only flow up, and so there is a hard cap on the number of serial steps that can be used to make a prediction.
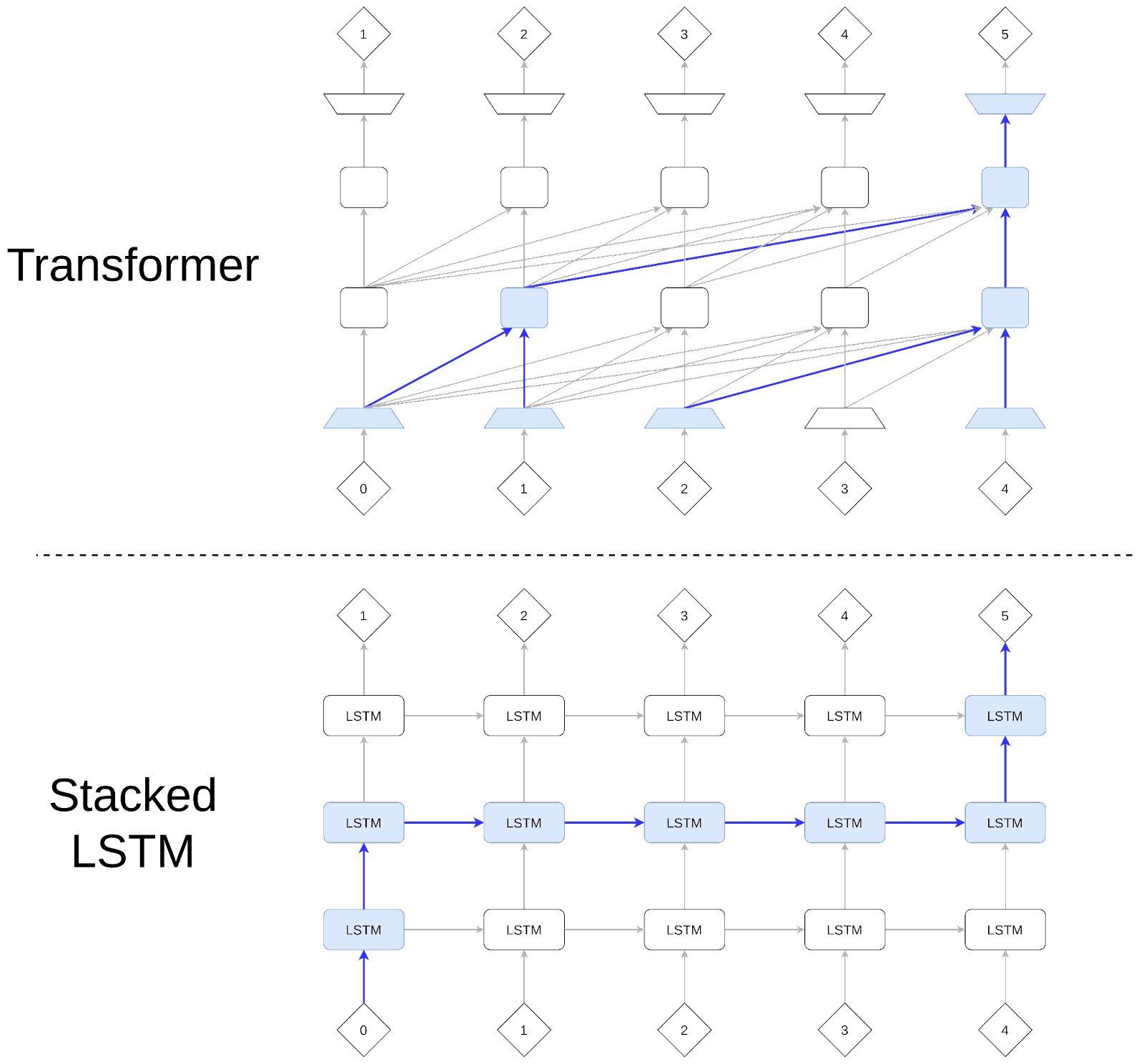
Here both a transformer and a stacked LSTM are shown predicting token 5 from the context (tokens 0-4). While each LSTM block is able to pass information to a copy of itself in the next column, in a transformer information can only be passed upward to the next layer.
Furthermore, the fact that a layer cannot pass information to itself is also a constraint which affects the inductive bias over possible search algorithms, likely disincentivizing algorithms that require certain subroutines to be reused many times for a single prediction. If weights are not being shared, then for a subroutine to be applied multiple times, it must be independently learned and implemented in different parts of the network. For example, if a search algorithm relies on something like an evaluation function, it would need to have separately learned every instance of its use, making the effective complexity of the algorithm’s description very high. This also might limit the extent to which we should expect to see algorithms which rely on recursion.
Another clue which restricts the algorithms we should expect from transformers relates to the way information seems to be processed in the residual stream. The transformer architecture relies on a residual stream, where individual heads read and write to a central channel of information. The logit lens appears to show that a byproduct of this design is that transformers tend to quickly find candidate solutions in early layers and then refine and update them over the rest of the forward pass. This might push us to consider algorithms that don’t completely depart from the solution space, and perhaps use early solutions to help inform the rest of the search process. For example, a transformer might exploit a certain duality between solution space and constraint space, iteratively using members of the solution space to identify constraints, and members of the constraint space to identify solutions.
Of course, it could also be that transformers are just using a giant bag of heuristics to produce solutions, and don’t implement anything at all like something we would call search. We can add credence to the existence of search processes by demonstrating the ability of transformers to solve “searchy” problems like chess, which seems to require a certain ability to search through possible futures, but ultimately what we really need is for interpretability to illuminate the difference.
How to Search for Search?
One thing that we would really like to have is a clear signal from reality that could help guide our thinking about this. We could spend a lot of time pondering the space of search algorithms, and which kind of algorithms a transformer might learn, but ultimately we would like some clear evidence to help narrow our questions. This seems like a really hard problem, and unfortunately the interpretability tools we currently have are limited, but here are some general thoughts about how to approach this problem.
Asking the right questions
We have to be able to turn abstract conceptual questions about search into testable hypotheses. One approach is to identify properties we expect learned search algorithms to have in theory, and then more concretely what computational artifacts we should expect to find in practice. We can do this both by considering what properties are sufficient or necessary for a search algorithm implemented within a particular architecture to function, as well as what is selected for by the training process.
We can then design experiments that make it possible to test those hypotheses. We can deliberately train transformers on “searchy” data, like maze solving or chess games, in order to focus on the types of search mechanisms that we think might make it possible to perform well on that data. For example, to predict chess games, it seems plausible that a transformer would need to consider future paths, and so we could focus our experiments there.
Failure modes
Many interpretability methods will try to determine what a neural network is thinking, and usually end up finding correlation rather than causation. For example, one can use some kind of supervised process to train a probe, and then use that probe to extract features from the activation space. Unfortunately this doesn’t guarantee that the network is actually using those features and not something which correlates with it. Furthermore, even if it does use those features, it might be using them in completely different ways than we expect. We end up trying to map our own ontology of information onto that of the neural network without really understanding it.
Take this paper, where the authors train linear probes to predict high-level chess features from the intermediate layers of AlphaZero in order to gain insight about what knowledge the network is using at various stages. They find that they are able to predict concepts like “king safety” and we could reason that this makes sense as a concept, as it could be useful for figuring out what moves to make next. But instead of picking up on king safety, the probe might also be picking up on other features, like the number of pieces on the board, which correlate strongly with king safety, and there isn’t an obvious way to tell the difference.
One way to overcome this is to focus on doing causal intervention, but even this has its problems. Semantic features are all intertwined and dependent on each other, and for many things it seems really non-trivial to edit something without breaking the network’s brain.[2] What would it mean to cause the network to believe the king was safe, without affecting a whole host of other semantic features? Is it possible to make a network trained on addition to think 2 + 2 = 5, without destroying its ability to do math?
Lastly, experiments often have the flaw of testing something more specific than the hypothesis we are actually interested in. We might often have a very general hypothesis about the kind of things the network might be doing, but end up implicitly testing a much more specific hypothesis. For example, we might hypothesize that a network is explicitly proposing candidates, but when we go to test it, our effective hypothesis becomes that the network is explicitly proposing candidates in a format that this method (e.g. linear probes) would find. If we get a negative result, we can’t say much about the original hypothesis because the network could just be doing things in a different way we aren’t able to detect. If we get a positive result, we might also just be picking up on some correlation which satisfies the test, but is actually caused by something fundamentally different from the original hypothesis.[3]
Firehose interpretability
Instead of designing experiments which deliver only a single bit of evidence (falsify/verify), another approach is to instead aim for methods which measure lots of things all at once, and produce a firehose of bits. If we don’t currently know the right questions to ask, or even in what ontology to pose our questions, then it can be really hard to design experiments that cut at the heart of what we care about, as well as to draw meaningful conclusions from them. When it becomes difficult to form testable hypotheses that make progress on the important questions, it makes sense to shift away from running classical hypothesis-driven experiments toward making high bit observations.
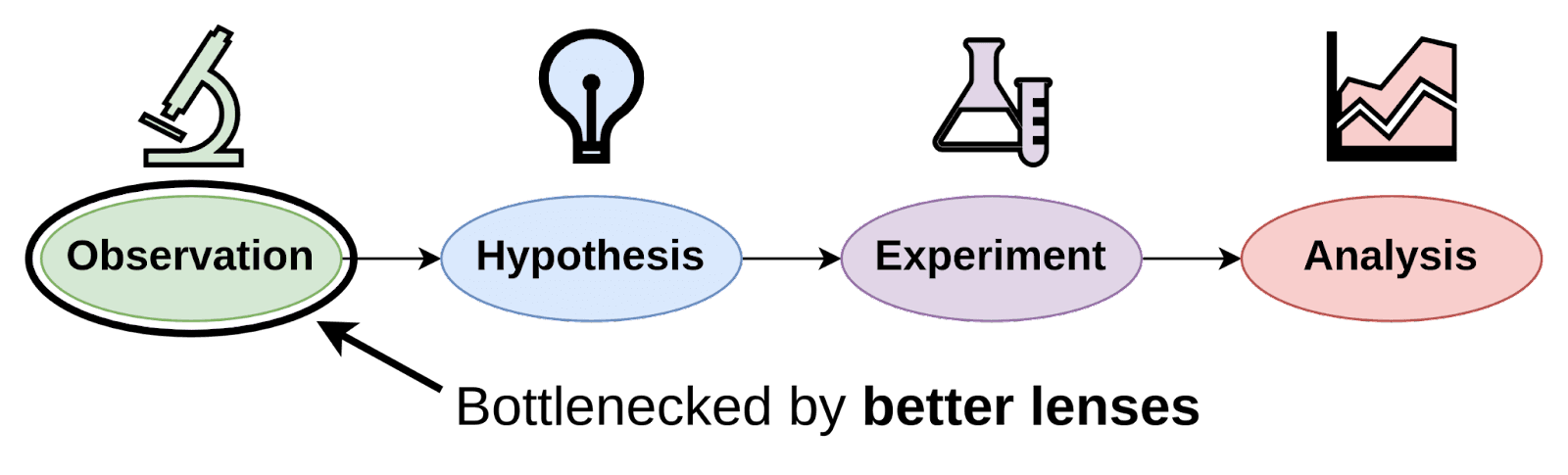
Our ability to make lots of useful observations depends on measurement tools, or lenses, that make visible things which are invisible, either by overcoming the physical limitations of our sense organs or our cognitive limitations to interpret raw data. This can be a major bottleneck to scientific progress, a prototypical example being the invention of the microscope, which was a turning point for our ability to study the natural world. The lenses that currently exist for interpretability are still quite crude, and expanding the current suite of tools, as well as building places to explore and visualize neural networks using those tools, seems critical for making lots of high bit observations.
Another motivation for high-bandwidth measurements comes from our problem with inferring causality from correlations. While it’s true that it’s impossible to determine causality from the correlation between just two variables, for more than two it can become possible, and the more variables we do measure the easier it becomes. This is a path to building causal models which avoids the pitfalls of intervening directly on a neural network.
Conclusion
Searching for search seems like an important research direction because it points at something strongly related to a lot of models for how misalignment happens, as well as being a prerequisite to a lot of potential solutions, like retargeting the search.
We want to be able to look for things like mesaoptimization or search, but when we look at a system and ask ourselves “is this system doing search?”, we realize that we don’t really understand the question. These words can make us feel like we know what we are talking about, but when we try to put them into practice we run into trouble. This is why it is so important to keep alignment research grounded in real-world AI systems: it forces us to confront what we don’t know, keeps us from getting lost speculating, and sharpens our focus.
We currently don’t really know where to look and which experiments will actually further our understanding, so figuring out how to translate these vague concepts into more concrete claims about how learned search happens on the algorithmic level is critical.
There are several papers which show this phenomenon, this paper being the most famous example.
Recent work from Jacques Thibodeau at SERI MATS and from the interpretability hackathon show evidence that editing factual knowledge with ROME does not robustly propagate logical implications and causes unintended side effects.
This problem of measuring something more specific than the thing we are interested in can also be addressed with auditing games.
Thanks to Dan Braun, Ze Shen Chin, Paul Colognese, Michael Ivanitskiy, Sudhanshu Kasewa, and Lucas Teixeira for feedback on drafts.
This work was carried out while at Conjecture.
This post is a loosely structured collection of thoughts and confusions about search and mesaoptimization and how to look for them in transformers. We've been thinking about this for a while and still feel confused. Hopefully this post makes others more confused so they can help.
Mesaoptimization
We can define mesaoptimization as internal optimization, where “optimization” describes the structure of computation within a system, not just its behavior. This kind of optimization seems particularly powerful, and many alignment researchers seem to think it’s one of the biggest concerns in alignment. Despite how important this is, we still understand very little about it.
For starters, it's not clear what internal optimization actually means. People have proposed several definitions of optimization which fit well when thinking about “behavioral optimization” where an agent acts to optimize its environment. One of the most clear and popular definitions comes from Alex Flint:
an optimizing system is a physical process in which the configuration of some part of the universe moves predictably towards a small set of target configurations from any point in a broad basin of optimization, despite perturbations during the optimization process.
In this framing, an agent and its environment together form an optimization process, where the agent acts upon the environment such that the system as a whole robustly converges to a set of target states.
But we run into problems when we try to map this behavioral definition to a definition about the structure of a process's internal computation. When we say mesaoptimization, we seem to mean something different than just that the computation converges to a smaller target. For example, an image classifier takes a large set of initial configurations of images including a lot of noise and irrelevant details, and layer by layer narrows it down to a probability distribution concentrated on a single class prediction. There seems to be a sense that this is not doing the kind of optimization we are concerned about when we talk about mesaoptimization.
Mesaoptimization was originally defined in Risks from Learned Optimization as internal search:
We will say that a system is an optimizer if it is internally searching through a search space (consisting of possible outputs, policies, plans, strategies, or similar) looking for those elements that score high according to some objective function that is explicitly represented within the system.
An advantage of this framing is that we do have some idea what we mean by “search” and have concrete examples of things which unambiguously qualify. Ideally, we’d like to point to the more general class of computation we’re worried about, but once you start thinking about what this general class of computation might look like, it quickly becomes clear that we don’t even know what “search” is. The space of search algorithms also seems much larger and more flexible than implied in the examples we usually think of.
At the moment we have very little idea what kind of algorithms we should expect neural networks to learn, and neither do we have a good picture of what kind of algorithms in particular we should be concerned about when we think of misalignment. If the intuition that “search” is somehow central to internal optimization holds validity, then becoming less confused about what learned search looks like should be central to making risks from internal optimization more concrete.
What is Search?
We have examples of processes which most would say are doing some kind of search, like Monte Carlo tree search, or A*, and processes that not everyone agrees count as search, like evolution through natural selection or stochastic gradient descent, which nonetheless clearly have search-like properties (the general disagreement about these examples is evidence that the concept is confusing). Some of these prototypical examples are handcrafted, others are natural, but broadly they operate in a similar way: They tend to generate candidate solutions, have a method for evaluating these candidate solutions, and use those evaluations to do a kind of iterative refinement of the solution space. This is highly reminiscent of what Abram Demski calls selection processes, which are able to both instantiate members of the solution space and obtain direct feedback on their quality.
While these are clearly doing search, this doesn’t look at all like how humans usually do search. Humans don’t restrict themselves to enumerating and evaluating candidate solutions. Instead, humans often operate over highly abstract compressions of the solution space, or search over entirely different spaces, such as global constraints on the problem, to make finding a solution more tractable.
Instead of focusing on one particular type of search, we want to think about the general properties that our examples of search share. At the highest level, they each take a large space of possible candidates (generally implicit to a problem specification) and shrink it down to a single solution which satisfies some criteria. If we say a process which finds a solution from a space of 2^N candidates can be thought of as doing N bits of optimization, then one place to start is to ask where those bits of optimization come from.
Compressing the search space
By transforming the search space into one which has significantly fewer degrees of freedom, we can quickly obtain a large number of bits, and shrink the scope of the problem down to one which is much more manageable.
Master chess players are able to better memorize boards by chunking structures of pieces as single units and converting a board to a higher level concept space not possessed by novices.[1] For instance, instead of separately tracking the positions of every pawn, the master player might memorize a single position for a group of pawns in a commonly-occurring arrangement.

This advantage is only present for real game positions, however, and completely disappears for fully random board states. This suggests that the concept space used by master players implicitly ignores most of the possible ways that the pieces can be arranged, and therefore has less degrees of freedom than the original space did. (It has to: for any lossless compression scheme, some possible sequences are inevitably incompressible, because there are fewer sequences of length < N than length N.)

Furthermore, unlike concepts representing literal "chunks" of relative positions parameterized by absolute position, many useful concepts may be invariant to the exact position of the pieces, like the concept of a “pin” or “skewer”. In practice this is a type of lossy compression which would not be able to disambiguate between possible boards if the differences are unlikely to be strategically relevant. The compression, more generally, is just a useful ontology, which makes the search problem significantly easier. Promising candidates (board positions or sequences of positions) can be represented in fewer bits, and the lower dimensional representation space can be used as a generator of candidates, because satisfactory solutions now make up a larger fraction of the now smaller compressed space.
This is important, because the way that the solution space gets compressed will shape what search looks like from the inside. Evaluated candidates may not be in the naive or expected representation, but rather be pointers to pieces of an internal ontology that might look very different. We should also expect those internal representations to be harder to detect and decipher, because the more a representation gets compressed, the more we should expect it to lose structural correlations which might distinguish it from noise.
Searching over constraint space
Another way to reduce the number of degrees of freedom is to focus on the constraints of a search problem. Searching over global constraints has many advantages, and seems to be one of the main ways humans search when the solution space is too large to reason about directly. Constraint space tends to be much lower dimensional, and can be used to implicitly carve out huge chunks of the original solution space, or break a problem down into smaller subproblems, allowing a search process to recurse on those subproblems, factoring the problem into manageable pieces. In a game like chess this might look like searching for threats, which operate like bottlenecks, requiring all successful plans to involve mitigating the threat as an instrumental subgoal.

This means that the candidates being considered may not map to solutions at all, instead being objects of an entirely different search space (e.g. that of threats). A search process might also consider solutions to smaller or relaxed subproblems, and never reference or relate directly to the full search target. This affects the problem of searching for search, because we might not be able to find the algorithm if we only search for signs of a search over solution space, such as instantiations of candidate solutions.
Another important quality of constraint space is that constraints are often useful for a wide range of search targets. For example, when planning a long distance trip, any successful plan will likely require booking a flight and going to the airport. This fact doesn’t depend very much on the exact destination, and so is especially useful to a more general purpose search process.
General purpose search, of the kind that humans possess, is also the kind of internal optimization that is most concerning and worth our study. Such a system would need to be able to take a search problem and actively simplify it by finding exploitable features of the search space at runtime, and breaking that problem down into more manageable subproblems.
Modularity and Retargetability
General purpose search needs to be able to take on a wide range of possible search problems and be flexible to distributional shifts. Systems which are robust to changes in the objective tend to be modular, composing their computation into submodules.

Non-modular systems, where the dependencies of computation are spread too widely to be split into distinct modules, are more likely to be brittle to changes in how the computation is performed. In learning to code, for example, a common early lesson is to split a program up into functions, and allow each function to interact with the rest of the program only through a small number of input and output variables (and avoid references to global variables). This doesn’t just make code easier to read, which is not a requirement for learned algorithms, but more importantly it contains the ripple effect that a change in one function has on the rest of the program.
This advantage of modularity applies both at runtime (reducing the chances that an uncommon input causes failure), as well as during development (reducing the number of changes needed to fix a bug). Analogously, we might expect modularity in learned algorithms both for their ability to generalize at runtime, as well as a part of the inductive bias of gradient descent. The more sprawling the dependencies, the more directions in the gradient landscape will lead directly to machinery breaking (and thus higher loss). A change to a module, on the other hand, need only be accompanied with a change to the API for the system as a whole to keep on functioning.
A likely place to find an example of modularity is in the retargetability of a search algorithm. If a search algorithm is general purpose, then the “target”, or what is being searched for, can’t be baked into or be implicit to the search process, but rather must be an input to a retargetable search algorithm. This applies to a system capable of handling a broad set of search problems, but even systems trained only to search with a single target have an incentive to be retargetable if that search algorithm breaks the problem down into subproblems, each with their own instrumental targets. If internal to the system there exists a target-agnostic search algorithm, with separate machinery for providing the target, then one place to start would be to find those modules (and understand how they interact with each other).
What even is a target/goal?
A target, through its interaction with the search algorithm, functions to “steer” search toward converging to a particular set of solutions. Much of the search process might be possible to do without any reference to the target (goal-agnostic preprocessing), but for general purpose algorithms we should expect a significant amount of the computation to hinge pivotally on the target.
In handcrafted search algorithms, the target has a clear type signature, and its interaction with the rest of the search process is well understood. In MCTS, for example, the target takes the shape of an evaluation function, and similarly for A*, the target is a coordinate which is used by a heuristic distance metric to guide the search process. They are both retargetable algorithms, and it’s easy to see how changing the target will change the process by which the algorithm will narrow the search space.
In learned search, it might be searching over multiple different ontologies, many of which don’t map to the solution space, as well as generate instrumental goals and recurse on subproblems. We don’t currently know what type signature the target would have, or how it slots into a search process to guide the computation, because we don’t have a good gears-level understanding of what learned search looks like.
Developing a better understanding of what targets are, both conceptually and experimentally, might give us a foot in the door toward understanding how targets interact with other modules within the search algorithm.
Learned Search in Transformers
Another angle of attack to understand mesaoptimization and search is to think about what types of algorithms we expect neural networks to learn. “Learned search” refers to search algorithms which, unlike handcrafted search algorithms, have been found automatically via gradient descent. If we find learned search within neural networks, it will need to conform both to the limitations of what can be implemented in the architecture as well as the inductive bias of gradient descent. Because of the success of LLMs like GPT-3 I’ll be focusing on the transformer architecture. Many of the arguments also apply to other architectures.
We might expect mesaoptimizers to be preferred for many reasons. Search at runtime is effectively a compressed version of a more complicated policy that encodes the information gained by search explicitly, specifying a system capable of generating that policy. For example, instead of memorizing a book of optimal chess openings, a program much shorter than the book could search through future consequences of moves and hypothetically converge to the same output.
There are, however, some reasons to be skeptical of finding search in transformers.
First of all, search isn’t free: the chess program that does brute-force search may have fewer lines of code, but is more expensive to run than a program that simply looks up a memorized answer. Any search algorithm which uses too much computation or memory just cannot be implemented by a transformer. This rules out many of the algorithms which rely heavily on explicitly enumerating and evaluating states. In the same vein, any algorithm that requires a high number of serial steps would also not be possible to run, even if the algorithm itself is in principle quite simple to describe. Unlike the NLP architectures that came before it, transformers are not recurrent. Information can only flow up, and so there is a hard cap on the number of serial steps that can be used to make a prediction.

Here both a transformer and a stacked LSTM are shown predicting token 5 from the context (tokens 0-4). While each LSTM block is able to pass information to a copy of itself in the next column, in a transformer information can only be passed upward to the next layer.
Furthermore, the fact that a layer cannot pass information to itself is also a constraint which affects the inductive bias over possible search algorithms, likely disincentivizing algorithms that require certain subroutines to be reused many times for a single prediction. If weights are not being shared, then for a subroutine to be applied multiple times, it must be independently learned and implemented in different parts of the network. For example, if a search algorithm relies on something like an evaluation function, it would need to have separately learned every instance of its use, making the effective complexity of the algorithm’s description very high. This also might limit the extent to which we should expect to see algorithms which rely on recursion.
Another clue which restricts the algorithms we should expect from transformers relates to the way information seems to be processed in the residual stream. The transformer architecture relies on a residual stream, where individual heads read and write to a central channel of information. The logit lens appears to show that a byproduct of this design is that transformers tend to quickly find candidate solutions in early layers and then refine and update them over the rest of the forward pass. This might push us to consider algorithms that don’t completely depart from the solution space, and perhaps use early solutions to help inform the rest of the search process. For example, a transformer might exploit a certain duality between solution space and constraint space, iteratively using members of the solution space to identify constraints, and members of the constraint space to identify solutions.
Of course, it could also be that transformers are just using a giant bag of heuristics to produce solutions, and don’t implement anything at all like something we would call search. We can add credence to the existence of search processes by demonstrating the ability of transformers to solve “searchy” problems like chess, which seems to require a certain ability to search through possible futures, but ultimately what we really need is for interpretability to illuminate the difference.
How to Search for Search?
One thing that we would really like to have is a clear signal from reality that could help guide our thinking about this. We could spend a lot of time pondering the space of search algorithms, and which kind of algorithms a transformer might learn, but ultimately we would like some clear evidence to help narrow our questions. This seems like a really hard problem, and unfortunately the interpretability tools we currently have are limited, but here are some general thoughts about how to approach this problem.
Asking the right questions
We have to be able to turn abstract conceptual questions about search into testable hypotheses. One approach is to identify properties we expect learned search algorithms to have in theory, and then more concretely what computational artifacts we should expect to find in practice. We can do this both by considering what properties are sufficient or necessary for a search algorithm implemented within a particular architecture to function, as well as what is selected for by the training process.
We can then design experiments that make it possible to test those hypotheses. We can deliberately train transformers on “searchy” data, like maze solving or chess games, in order to focus on the types of search mechanisms that we think might make it possible to perform well on that data. For example, to predict chess games, it seems plausible that a transformer would need to consider future paths, and so we could focus our experiments there.
Failure modes
Many interpretability methods will try to determine what a neural network is thinking, and usually end up finding correlation rather than causation. For example, one can use some kind of supervised process to train a probe, and then use that probe to extract features from the activation space. Unfortunately this doesn’t guarantee that the network is actually using those features and not something which correlates with it. Furthermore, even if it does use those features, it might be using them in completely different ways than we expect. We end up trying to map our own ontology of information onto that of the neural network without really understanding it.
Take this paper, where the authors train linear probes to predict high-level chess features from the intermediate layers of AlphaZero in order to gain insight about what knowledge the network is using at various stages. They find that they are able to predict concepts like “king safety” and we could reason that this makes sense as a concept, as it could be useful for figuring out what moves to make next. But instead of picking up on king safety, the probe might also be picking up on other features, like the number of pieces on the board, which correlate strongly with king safety, and there isn’t an obvious way to tell the difference.
One way to overcome this is to focus on doing causal intervention, but even this has its problems. Semantic features are all intertwined and dependent on each other, and for many things it seems really non-trivial to edit something without breaking the network’s brain.[2] What would it mean to cause the network to believe the king was safe, without affecting a whole host of other semantic features? Is it possible to make a network trained on addition to think 2 + 2 = 5, without destroying its ability to do math?
Lastly, experiments often have the flaw of testing something more specific than the hypothesis we are actually interested in. We might often have a very general hypothesis about the kind of things the network might be doing, but end up implicitly testing a much more specific hypothesis. For example, we might hypothesize that a network is explicitly proposing candidates, but when we go to test it, our effective hypothesis becomes that the network is explicitly proposing candidates in a format that this method (e.g. linear probes) would find. If we get a negative result, we can’t say much about the original hypothesis because the network could just be doing things in a different way we aren’t able to detect. If we get a positive result, we might also just be picking up on some correlation which satisfies the test, but is actually caused by something fundamentally different from the original hypothesis.[3]
Firehose interpretability
Instead of designing experiments which deliver only a single bit of evidence (falsify/verify), another approach is to instead aim for methods which measure lots of things all at once, and produce a firehose of bits. If we don’t currently know the right questions to ask, or even in what ontology to pose our questions, then it can be really hard to design experiments that cut at the heart of what we care about, as well as to draw meaningful conclusions from them. When it becomes difficult to form testable hypotheses that make progress on the important questions, it makes sense to shift away from running classical hypothesis-driven experiments toward making high bit observations.

Our ability to make lots of useful observations depends on measurement tools, or lenses, that make visible things which are invisible, either by overcoming the physical limitations of our sense organs or our cognitive limitations to interpret raw data. This can be a major bottleneck to scientific progress, a prototypical example being the invention of the microscope, which was a turning point for our ability to study the natural world. The lenses that currently exist for interpretability are still quite crude, and expanding the current suite of tools, as well as building places to explore and visualize neural networks using those tools, seems critical for making lots of high bit observations.
Another motivation for high-bandwidth measurements comes from our problem with inferring causality from correlations. While it’s true that it’s impossible to determine causality from the correlation between just two variables, for more than two it can become possible, and the more variables we do measure the easier it becomes. This is a path to building causal models which avoids the pitfalls of intervening directly on a neural network.
Conclusion
Searching for search seems like an important research direction because it points at something strongly related to a lot of models for how misalignment happens, as well as being a prerequisite to a lot of potential solutions, like retargeting the search.
We want to be able to look for things like mesaoptimization or search, but when we look at a system and ask ourselves “is this system doing search?”, we realize that we don’t really understand the question. These words can make us feel like we know what we are talking about, but when we try to put them into practice we run into trouble. This is why it is so important to keep alignment research grounded in real-world AI systems: it forces us to confront what we don’t know, keeps us from getting lost speculating, and sharpens our focus.
We currently don’t really know where to look and which experiments will actually further our understanding, so figuring out how to translate these vague concepts into more concrete claims about how learned search happens on the algorithmic level is critical.
There are several papers which show this phenomenon, this paper being the most famous example.
Recent work from Jacques Thibodeau at SERI MATS and from the interpretability hackathon show evidence that editing factual knowledge with ROME does not robustly propagate logical implications and causes unintended side effects.
This problem of measuring something more specific than the thing we are interested in can also be addressed with auditing games.
Thanks to Dan Braun, Ze Shen Chin, Paul Colognese, Michael Ivanitskiy, Sudhanshu Kasewa, and Lucas Teixeira for feedback on drafts.
This work was carried out while at Conjecture.
This post is a loosely structured collection of thoughts and confusions about search and mesaoptimization and how to look for them in transformers. We've been thinking about this for a while and still feel confused. Hopefully this post makes others more confused so they can help.
Mesaoptimization
We can define mesaoptimization as internal optimization, where “optimization” describes the structure of computation within a system, not just its behavior. This kind of optimization seems particularly powerful, and many alignment researchers seem to think it’s one of the biggest concerns in alignment. Despite how important this is, we still understand very little about it.
For starters, it's not clear what internal optimization actually means. People have proposed several definitions of optimization which fit well when thinking about “behavioral optimization” where an agent acts to optimize its environment. One of the most clear and popular definitions comes from Alex Flint:
an optimizing system is a physical process in which the configuration of some part of the universe moves predictably towards a small set of target configurations from any point in a broad basin of optimization, despite perturbations during the optimization process.
In this framing, an agent and its environment together form an optimization process, where the agent acts upon the environment such that the system as a whole robustly converges to a set of target states.
But we run into problems when we try to map this behavioral definition to a definition about the structure of a process's internal computation. When we say mesaoptimization, we seem to mean something different than just that the computation converges to a smaller target. For example, an image classifier takes a large set of initial configurations of images including a lot of noise and irrelevant details, and layer by layer narrows it down to a probability distribution concentrated on a single class prediction. There seems to be a sense that this is not doing the kind of optimization we are concerned about when we talk about mesaoptimization.
Mesaoptimization was originally defined in Risks from Learned Optimization as internal search:
We will say that a system is an optimizer if it is internally searching through a search space (consisting of possible outputs, policies, plans, strategies, or similar) looking for those elements that score high according to some objective function that is explicitly represented within the system.
An advantage of this framing is that we do have some idea what we mean by “search” and have concrete examples of things which unambiguously qualify. Ideally, we’d like to point to the more general class of computation we’re worried about, but once you start thinking about what this general class of computation might look like, it quickly becomes clear that we don’t even know what “search” is. The space of search algorithms also seems much larger and more flexible than implied in the examples we usually think of.
At the moment we have very little idea what kind of algorithms we should expect neural networks to learn, and neither do we have a good picture of what kind of algorithms in particular we should be concerned about when we think of misalignment. If the intuition that “search” is somehow central to internal optimization holds validity, then becoming less confused about what learned search looks like should be central to making risks from internal optimization more concrete.
What is Search?
We have examples of processes which most would say are doing some kind of search, like Monte Carlo tree search, or A*, and processes that not everyone agrees count as search, like evolution through natural selection or stochastic gradient descent, which nonetheless clearly have search-like properties (the general disagreement about these examples is evidence that the concept is confusing). Some of these prototypical examples are handcrafted, others are natural, but broadly they operate in a similar way: They tend to generate candidate solutions, have a method for evaluating these candidate solutions, and use those evaluations to do a kind of iterative refinement of the solution space. This is highly reminiscent of what Abram Demski calls selection processes, which are able to both instantiate members of the solution space and obtain direct feedback on their quality.
While these are clearly doing search, this doesn’t look at all like how humans usually do search. Humans don’t restrict themselves to enumerating and evaluating candidate solutions. Instead, humans often operate over highly abstract compressions of the solution space, or search over entirely different spaces, such as global constraints on the problem, to make finding a solution more tractable.
Instead of focusing on one particular type of search, we want to think about the general properties that our examples of search share. At the highest level, they each take a large space of possible candidates (generally implicit to a problem specification) and shrink it down to a single solution which satisfies some criteria. If we say a process which finds a solution from a space of 2^N candidates can be thought of as doing N bits of optimization, then one place to start is to ask where those bits of optimization come from.
Compressing the search space
By transforming the search space into one which has significantly fewer degrees of freedom, we can quickly obtain a large number of bits, and shrink the scope of the problem down to one which is much more manageable.
Master chess players are able to better memorize boards by chunking structures of pieces as single units and converting a board to a higher level concept space not possessed by novices.[1] For instance, instead of separately tracking the positions of every pawn, the master player might memorize a single position for a group of pawns in a commonly-occurring arrangement.

This advantage is only present for real game positions, however, and completely disappears for fully random board states. This suggests that the concept space used by master players implicitly ignores most of the possible ways that the pieces can be arranged, and therefore has less degrees of freedom than the original space did. (It has to: for any lossless compression scheme, some possible sequences are inevitably incompressible, because there are fewer sequences of length < N than length N.)

Furthermore, unlike concepts representing literal "chunks" of relative positions parameterized by absolute position, many useful concepts may be invariant to the exact position of the pieces, like the concept of a “pin” or “skewer”. In practice this is a type of lossy compression which would not be able to disambiguate between possible boards if the differences are unlikely to be strategically relevant. The compression, more generally, is just a useful ontology, which makes the search problem significantly easier. Promising candidates (board positions or sequences of positions) can be represented in fewer bits, and the lower dimensional representation space can be used as a generator of candidates, because satisfactory solutions now make up a larger fraction of the now smaller compressed space.
This is important, because the way that the solution space gets compressed will shape what search looks like from the inside. Evaluated candidates may not be in the naive or expected representation, but rather be pointers to pieces of an internal ontology that might look very different. We should also expect those internal representations to be harder to detect and decipher, because the more a representation gets compressed, the more we should expect it to lose structural correlations which might distinguish it from noise.
Searching over constraint space
Another way to reduce the number of degrees of freedom is to focus on the constraints of a search problem. Searching over global constraints has many advantages, and seems to be one of the main ways humans search when the solution space is too large to reason about directly. Constraint space tends to be much lower dimensional, and can be used to implicitly carve out huge chunks of the original solution space, or break a problem down into smaller subproblems, allowing a search process to recurse on those subproblems, factoring the problem into manageable pieces. In a game like chess this might look like searching for threats, which operate like bottlenecks, requiring all successful plans to involve mitigating the threat as an instrumental subgoal.

This means that the candidates being considered may not map to solutions at all, instead being objects of an entirely different search space (e.g. that of threats). A search process might also consider solutions to smaller or relaxed subproblems, and never reference or relate directly to the full search target. This affects the problem of searching for search, because we might not be able to find the algorithm if we only search for signs of a search over solution space, such as instantiations of candidate solutions.
Another important quality of constraint space is that constraints are often useful for a wide range of search targets. For example, when planning a long distance trip, any successful plan will likely require booking a flight and going to the airport. This fact doesn’t depend very much on the exact destination, and so is especially useful to a more general purpose search process.
General purpose search, of the kind that humans possess, is also the kind of internal optimization that is most concerning and worth our study. Such a system would need to be able to take a search problem and actively simplify it by finding exploitable features of the search space at runtime, and breaking that problem down into more manageable subproblems.
Modularity and Retargetability
General purpose search needs to be able to take on a wide range of possible search problems and be flexible to distributional shifts. Systems which are robust to changes in the objective tend to be modular, composing their computation into submodules.

Non-modular systems, where the dependencies of computation are spread too widely to be split into distinct modules, are more likely to be brittle to changes in how the computation is performed. In learning to code, for example, a common early lesson is to split a program up into functions, and allow each function to interact with the rest of the program only through a small number of input and output variables (and avoid references to global variables). This doesn’t just make code easier to read, which is not a requirement for learned algorithms, but more importantly it contains the ripple effect that a change in one function has on the rest of the program.
This advantage of modularity applies both at runtime (reducing the chances that an uncommon input causes failure), as well as during development (reducing the number of changes needed to fix a bug). Analogously, we might expect modularity in learned algorithms both for their ability to generalize at runtime, as well as a part of the inductive bias of gradient descent. The more sprawling the dependencies, the more directions in the gradient landscape will lead directly to machinery breaking (and thus higher loss). A change to a module, on the other hand, need only be accompanied with a change to the API for the system as a whole to keep on functioning.
A likely place to find an example of modularity is in the retargetability of a search algorithm. If a search algorithm is general purpose, then the “target”, or what is being searched for, can’t be baked into or be implicit to the search process, but rather must be an input to a retargetable search algorithm. This applies to a system capable of handling a broad set of search problems, but even systems trained only to search with a single target have an incentive to be retargetable if that search algorithm breaks the problem down into subproblems, each with their own instrumental targets. If internal to the system there exists a target-agnostic search algorithm, with separate machinery for providing the target, then one place to start would be to find those modules (and understand how they interact with each other).
What even is a target/goal?
A target, through its interaction with the search algorithm, functions to “steer” search toward converging to a particular set of solutions. Much of the search process might be possible to do without any reference to the target (goal-agnostic preprocessing), but for general purpose algorithms we should expect a significant amount of the computation to hinge pivotally on the target.
In handcrafted search algorithms, the target has a clear type signature, and its interaction with the rest of the search process is well understood. In MCTS, for example, the target takes the shape of an evaluation function, and similarly for A*, the target is a coordinate which is used by a heuristic distance metric to guide the search process. They are both retargetable algorithms, and it’s easy to see how changing the target will change the process by which the algorithm will narrow the search space.
In learned search, it might be searching over multiple different ontologies, many of which don’t map to the solution space, as well as generate instrumental goals and recurse on subproblems. We don’t currently know what type signature the target would have, or how it slots into a search process to guide the computation, because we don’t have a good gears-level understanding of what learned search looks like.
Developing a better understanding of what targets are, both conceptually and experimentally, might give us a foot in the door toward understanding how targets interact with other modules within the search algorithm.
Learned Search in Transformers
Another angle of attack to understand mesaoptimization and search is to think about what types of algorithms we expect neural networks to learn. “Learned search” refers to search algorithms which, unlike handcrafted search algorithms, have been found automatically via gradient descent. If we find learned search within neural networks, it will need to conform both to the limitations of what can be implemented in the architecture as well as the inductive bias of gradient descent. Because of the success of LLMs like GPT-3 I’ll be focusing on the transformer architecture. Many of the arguments also apply to other architectures.
We might expect mesaoptimizers to be preferred for many reasons. Search at runtime is effectively a compressed version of a more complicated policy that encodes the information gained by search explicitly, specifying a system capable of generating that policy. For example, instead of memorizing a book of optimal chess openings, a program much shorter than the book could search through future consequences of moves and hypothetically converge to the same output.
There are, however, some reasons to be skeptical of finding search in transformers.
First of all, search isn’t free: the chess program that does brute-force search may have fewer lines of code, but is more expensive to run than a program that simply looks up a memorized answer. Any search algorithm which uses too much computation or memory just cannot be implemented by a transformer. This rules out many of the algorithms which rely heavily on explicitly enumerating and evaluating states. In the same vein, any algorithm that requires a high number of serial steps would also not be possible to run, even if the algorithm itself is in principle quite simple to describe. Unlike the NLP architectures that came before it, transformers are not recurrent. Information can only flow up, and so there is a hard cap on the number of serial steps that can be used to make a prediction.

Here both a transformer and a stacked LSTM are shown predicting token 5 from the context (tokens 0-4). While each LSTM block is able to pass information to a copy of itself in the next column, in a transformer information can only be passed upward to the next layer.
Furthermore, the fact that a layer cannot pass information to itself is also a constraint which affects the inductive bias over possible search algorithms, likely disincentivizing algorithms that require certain subroutines to be reused many times for a single prediction. If weights are not being shared, then for a subroutine to be applied multiple times, it must be independently learned and implemented in different parts of the network. For example, if a search algorithm relies on something like an evaluation function, it would need to have separately learned every instance of its use, making the effective complexity of the algorithm’s description very high. This also might limit the extent to which we should expect to see algorithms which rely on recursion.
Another clue which restricts the algorithms we should expect from transformers relates to the way information seems to be processed in the residual stream. The transformer architecture relies on a residual stream, where individual heads read and write to a central channel of information. The logit lens appears to show that a byproduct of this design is that transformers tend to quickly find candidate solutions in early layers and then refine and update them over the rest of the forward pass. This might push us to consider algorithms that don’t completely depart from the solution space, and perhaps use early solutions to help inform the rest of the search process. For example, a transformer might exploit a certain duality between solution space and constraint space, iteratively using members of the solution space to identify constraints, and members of the constraint space to identify solutions.
Of course, it could also be that transformers are just using a giant bag of heuristics to produce solutions, and don’t implement anything at all like something we would call search. We can add credence to the existence of search processes by demonstrating the ability of transformers to solve “searchy” problems like chess, which seems to require a certain ability to search through possible futures, but ultimately what we really need is for interpretability to illuminate the difference.
How to Search for Search?
One thing that we would really like to have is a clear signal from reality that could help guide our thinking about this. We could spend a lot of time pondering the space of search algorithms, and which kind of algorithms a transformer might learn, but ultimately we would like some clear evidence to help narrow our questions. This seems like a really hard problem, and unfortunately the interpretability tools we currently have are limited, but here are some general thoughts about how to approach this problem.
Asking the right questions
We have to be able to turn abstract conceptual questions about search into testable hypotheses. One approach is to identify properties we expect learned search algorithms to have in theory, and then more concretely what computational artifacts we should expect to find in practice. We can do this both by considering what properties are sufficient or necessary for a search algorithm implemented within a particular architecture to function, as well as what is selected for by the training process.
We can then design experiments that make it possible to test those hypotheses. We can deliberately train transformers on “searchy” data, like maze solving or chess games, in order to focus on the types of search mechanisms that we think might make it possible to perform well on that data. For example, to predict chess games, it seems plausible that a transformer would need to consider future paths, and so we could focus our experiments there.
Failure modes
Many interpretability methods will try to determine what a neural network is thinking, and usually end up finding correlation rather than causation. For example, one can use some kind of supervised process to train a probe, and then use that probe to extract features from the activation space. Unfortunately this doesn’t guarantee that the network is actually using those features and not something which correlates with it. Furthermore, even if it does use those features, it might be using them in completely different ways than we expect. We end up trying to map our own ontology of information onto that of the neural network without really understanding it.
Take this paper, where the authors train linear probes to predict high-level chess features from the intermediate layers of AlphaZero in order to gain insight about what knowledge the network is using at various stages. They find that they are able to predict concepts like “king safety” and we could reason that this makes sense as a concept, as it could be useful for figuring out what moves to make next. But instead of picking up on king safety, the probe might also be picking up on other features, like the number of pieces on the board, which correlate strongly with king safety, and there isn’t an obvious way to tell the difference.
One way to overcome this is to focus on doing causal intervention, but even this has its problems. Semantic features are all intertwined and dependent on each other, and for many things it seems really non-trivial to edit something without breaking the network’s brain.[2] What would it mean to cause the network to believe the king was safe, without affecting a whole host of other semantic features? Is it possible to make a network trained on addition to think 2 + 2 = 5, without destroying its ability to do math?
Lastly, experiments often have the flaw of testing something more specific than the hypothesis we are actually interested in. We might often have a very general hypothesis about the kind of things the network might be doing, but end up implicitly testing a much more specific hypothesis. For example, we might hypothesize that a network is explicitly proposing candidates, but when we go to test it, our effective hypothesis becomes that the network is explicitly proposing candidates in a format that this method (e.g. linear probes) would find. If we get a negative result, we can’t say much about the original hypothesis because the network could just be doing things in a different way we aren’t able to detect. If we get a positive result, we might also just be picking up on some correlation which satisfies the test, but is actually caused by something fundamentally different from the original hypothesis.[3]
Firehose interpretability
Instead of designing experiments which deliver only a single bit of evidence (falsify/verify), another approach is to instead aim for methods which measure lots of things all at once, and produce a firehose of bits. If we don’t currently know the right questions to ask, or even in what ontology to pose our questions, then it can be really hard to design experiments that cut at the heart of what we care about, as well as to draw meaningful conclusions from them. When it becomes difficult to form testable hypotheses that make progress on the important questions, it makes sense to shift away from running classical hypothesis-driven experiments toward making high bit observations.

Our ability to make lots of useful observations depends on measurement tools, or lenses, that make visible things which are invisible, either by overcoming the physical limitations of our sense organs or our cognitive limitations to interpret raw data. This can be a major bottleneck to scientific progress, a prototypical example being the invention of the microscope, which was a turning point for our ability to study the natural world. The lenses that currently exist for interpretability are still quite crude, and expanding the current suite of tools, as well as building places to explore and visualize neural networks using those tools, seems critical for making lots of high bit observations.
Another motivation for high-bandwidth measurements comes from our problem with inferring causality from correlations. While it’s true that it’s impossible to determine causality from the correlation between just two variables, for more than two it can become possible, and the more variables we do measure the easier it becomes. This is a path to building causal models which avoids the pitfalls of intervening directly on a neural network.
Conclusion
Searching for search seems like an important research direction because it points at something strongly related to a lot of models for how misalignment happens, as well as being a prerequisite to a lot of potential solutions, like retargeting the search.
We want to be able to look for things like mesaoptimization or search, but when we look at a system and ask ourselves “is this system doing search?”, we realize that we don’t really understand the question. These words can make us feel like we know what we are talking about, but when we try to put them into practice we run into trouble. This is why it is so important to keep alignment research grounded in real-world AI systems: it forces us to confront what we don’t know, keeps us from getting lost speculating, and sharpens our focus.
We currently don’t really know where to look and which experiments will actually further our understanding, so figuring out how to translate these vague concepts into more concrete claims about how learned search happens on the algorithmic level is critical.
There are several papers which show this phenomenon, this paper being the most famous example.
Recent work from Jacques Thibodeau at SERI MATS and from the interpretability hackathon show evidence that editing factual knowledge with ROME does not robustly propagate logical implications and causes unintended side effects.
This problem of measuring something more specific than the thing we are interested in can also be addressed with auditing games.
Latest Articles




Dec 2, 2024
Conjecture: A Roadmap for Cognitive Software and A Humanist Future of AI
Conjecture: A Roadmap for Cognitive Software and A Humanist Future of AI
An overview of Conjecture's approach to "Cognitive Software," and our build path towards a good future.
Feb 24, 2024
Christiano (ARC) and GA (Conjecture) Discuss Alignment Cruxes
Christiano (ARC) and GA (Conjecture) Discuss Alignment Cruxes
The following are the summary and transcript of a discussion between Paul Christiano (ARC) and Gabriel Alfour, hereafter GA (Conjecture), which took place on December 11, 2022 on Slack. It was held as part of a series of discussions between Conjecture and people from other organizations in the AGI and alignment field. See our retrospective on the Discussions for more information about the project and the format.




Feb 15, 2024
Conjecture: 2 Years
Conjecture: 2 Years
It has been 2 years since a group of hackers and idealists from across the globe gathered into a tiny, oxygen-deprived coworking space in downtown London with one goal in mind: Make the future go well, for everybody. And so, Conjecture was born.
Sign up to receive our newsletter and
updates on products and services.
Sign up to receive our newsletter and updates on products and services.
Sign up to receive our newsletter and updates on products and services.